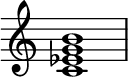Minor seventh chord
| Component intervals from root | |
|---|---|
| minor seventh | |
| perfect fifth | |
| minor third | |
| root | |
| Tuning | |
| 10:12:15:18[1] | |
| Forte no. / | |
| 4-26 / |
In music, a minor seventh chord is a seventh chord composed of a root note, a minor third, a perfect fifth, and a minor seventh (1, ♭3, 5, ♭7). In other words, one could think of it as a minor triad with a minor seventh attached to it.[2]
For example, the minor seventh chord built on A, commonly written as A−7, has pitches A-C-E-G:
Minor/minor seventh chord
[edit]A seventh chord with a minor third, perfect fifth, and minor seventh is commonly called a minor seventh chord, but also sometimes a minor/minor seventh chord to distinguish it from the minor/major seventh chord discussed below. It can be represented as either as m7 or −7, or in integer notation, {0, 3, 7, 10}.
This chord occurs on different scale degrees in different diatonic scales:
- In a major scale, it is on the supertonic, mediant, and submediant degrees (
, 
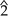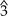, and 
).[3] This is why the ii in a ii–V–I turnaround is a minor seventh chord (ii7).
- In a natural minor scale, it is on the tonic, subdominant, and dominant degrees (
, 
, and 
).[4] - In a harmonic minor scale, it is only on the subdominant degree ().[4]
- In an ascending melodic minor scale, it is only on the supertonic degree (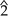).[4]
Example of tonic minor seventh chords include LaBelle's "Lady Marmalade", Roberta Flack's "Killing Me Softly with His Song", The Doobie Brothers' "Long Train Runnin'", Chic's "Le Freak", Lipps Inc.'s "Funkytown", and the Eagles' "One Of These Nights".[5]
The major sixth chord (major triad with an added major sixth) is an inversion of this chord.
Minor/major seventh chord
[edit]When the seventh note is a major seventh above the root, it is called a minor/major seventh chord. For example, the minor/major seventh chord built on C, commonly written as CmM7, has pitches C–E♭–G–B:
Its harmonic function is similar to that of a "normal" minor seventh, as is the minor seven flat five or half-diminished chord – but in each case, the altered tone (seventh or fifth, respectively) creates a different feeling which is exploited in modulations and to use leading-tones.
Minor seventh as virtual augmented sixth chord
[edit]The minor seventh chord may also have its interval of minor seventh (between root and seventh degree, i.e.: C–B♭ in C–E♭–G–B♭) rewritten as an augmented sixth C–E♭–G–A♯.[6] Rearranging and transposing, this gives A♭–C♭–E♭–F♯, a virtual minor version of the German augmented sixth chord.[7] Again like the typical augmented sixth, this enharmonic interpretation gives on a resolution irregular for the minor seventh but normal for the augmented sixth chord, where the 2 voices at the enharmonic major second converge to unison or diverge to octave.[8]
Minor seventh chord table
[edit]Chord Root Minor third Perfect fifth Minor seventh Cm7 C E♭ G B♭ C♯m7 C♯ E G♯ B D♭m7 D♭ F♭ A♭ C♭ Dm7 D F A C D♯m7 D♯ F♯ A♯ C♯ E♭m7 E♭ G♭ B♭ D♭ Em7 E G B D Fm7 F A♭ C E♭ F♯m7 F♯ A C♯ E G♭m7 G♭ B 
D♭ F♭ Gm7 G B♭ D F G♯m7 G♯ B D♯ F♯ A♭m7 A♭ C♭ E♭ G♭ Am7 A C E G A♯m7 A♯ C♯ E♯ G♯ B♭m7 B♭ D♭ F A♭ Bm7 B D F♯ A
The just minor seventh chord is tuned in the ratios 10:12:15:18.[9] This may be found on iii, vi, and vii.[10] Another tuning may be in the ratios 48:40:32:27.[11]
Minor seventh chords for guitar
[edit]In standard tuning, the left is the low E string, the number is the fret, and x means mute the string.
References
[edit]- ^ Shirlaw, Matthew (1900). The Theory of Harmony, p.86. ISBN 978-1-4510-1534-8.
- ^ "musictheory.net". www.musictheory.net. Retrieved 2024-01-30.
- ^ Benward & Saker (2003), p.229.
- ^ a b c Benward & Saker (2003). Music: In Theory and Practice, Vol. I, p.230. Seventh Edition. ISBN 978-0-07-294262-0.
- ^ Stephenson, Ken (2002). What to Listen for in Rock: A Stylistic Analysis, p.83. ISBN 978-0-300-09239-4.
- ^ Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 137, Oxford, Clarendon Press.
- ^ Ouseley, Frederick. A. Gore (1868). A Treatise on Harmony, pg. 143ff, Oxford, Clarendon Press.
- ^ Christ, William (1966). Materials and Structure of Music, v.2, p. 154. Englewood Cliffs: Prentice-Hall. LOC 66-14354.
- ^ David Wright (2009). Mathematics and Music, p.141. ISBN 978-0-8218-4873-9.
- ^ Wright, David (2009). Mathematics and Music, p.140-41. ISBN 978-0-8218-4873-9.
- ^ François-Joseph Fétis and Mary I. Arlin (1994). Esquisse de l'histoire de l'harmonie, p.97n55. ISBN 0-945193-51-3.
- ^ "Reverse Guitar Chord Name Finder With Sound, Vertical Fretboard".
- ^ "Minor 7th Chords".
- ^ "Music | audiopologie". Archived from the original on 2017-12-10. Retrieved 2017-12-17.
